Grundoperationen

Grundrechenarten und ihre Zeichen

Grundoperationen

Addition

• + ist das Pluszeichen.
• Summand + Summand = Summe
• Hier gelten das Kommutativgesetz und das Assoziativgesetz.

Subtraktion

• − ist das Minuszeichen.
• Minuend − Subtrahend = Differenz

Multiplikation

• × ist das Malzeichen.
• Faktor × Faktor = Produkt
• Hier gelten das Kommutativgesetz, das Assoziativgesetz und die Punkt-vor-Strich-Regel.

Division

• : ist das Geteiltzeichen.
• Dividend : Divisor = Quotient
• Hier gilt ebenfalls die Punkt-vor-Strich-Regel.

Brüche

Ein Bruch wird wie folgt dargestellt: 5/2

• Die Linie in der Mitte nennt man Bruchstrich.
• Die obere Zahl ist der Zähler, die untere Zahl der Nenner.
• Brüche erfüllen denselben Zweck wie Divisionen.

Regeln zu Brüchen werden in einem separaten Kapitel erklärt.

Potenz

Eine Potenz hat kein spezielles Symbol, aber eine bestimmte Schreibweise, z. B. 5².

• Die untere Zahl ist die Basis.
• Die obere Zahl ist der Exponent.
• Das Ergebnis wird Potenzwert genannt.

Wurzel

Das Wurzelzeichen ist √.

• Die Zahl über dem Anfang des Wurzelzeichens nennt man Wurzelexponent.
• Die Zahl unter dem Zeichen ist der Radikand.
• Das Ergebnis, ohne das Wurzelzeichen geschrieben, heißt Wurzelwert.

Gesetze der Mathematik

Kommutativgesetz

• Die Reihenfolge der Zahlen spielt bei Addition und Multiplikation keine Rolle.

Beispiel:

• Addition: 2+3=3+22 + 3 = 3 + 22+3=3+2
• Multiplikation: 2×3=3×22 × 3 = 3 × 22×3=3×2
• Dieses Gesetz gilt nicht für Subtraktion und Division:
  • 2−3≠3−22 – 3 ≠ 3 – 22−3=3−2
  • 3:2≠2:33 : 2 ≠ 2 : 33:2=2:3

Assoziativgesetz

• Die Platzierung von Klammern ist bei Addition und Multiplikation beliebig.

Beispiel:

• Addition: (2+3)+4=2+(3+4)(2 + 3) + 4 = 2 + (3 + 4)(2+3)+4=2+(3+4)
• Multiplikation: (2×3)×4=2×(3×4)(2 × 3) × 4 = 2 × (3 × 4)(2×3)×4=2×(3×4)
• Dieses Gesetz gilt nicht für Subtraktion und Division:
  • (2−3)−4≠2−(3−4)(2 – 3) – 4 ≠ 2 – (3 – 4)(2−3)−4=2−(3−4)
  • (2:3):4≠2:(3:4)(2 : 3) : 4 ≠ 2 : (3 : 4)(2:3):4=2:(3:4)

Punkt-vor-Strich-Regel

• Multiplikationen und Divisionen haben Vorrang vor Additionen und Subtraktionen.

Beispiel:            2+3×42 + 3 × 42+3×4: Zuerst wird 3×43 × 43×4 berechnet, dann das Ergebnis zu 222 addiert.

Distributivgesetz

• Eine Zahl kann auf eine Summe oder Differenz in einer Klammer verteilt werden.

Beispiel:            (2+3)×4=2×4+3×4(2 + 3) × 4 = 2 × 4 + 3 × 4(2+3)×4=2×4+3×4

Ausklammerungsgesetz

• Dieses Gesetz ist die Umkehrung des Distributivgesetzes.
• Gleiche Faktoren können ausgeklammert werden.

Beispiel:            8+12=2×4+3×4=(2+3)×48 + 12 = 2 × 4 + 3 × 4 = (2 + 3) × 48+12=2×4+3×4=(2+3)×4

Produktregel für Wurzel

• Die Wurzel eines Produkts ist das Produkt der einzelnen Wurzeln.

Beispiel:           

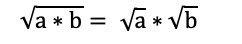
Quotientenregel für Wurzeln

• Die Wurzel eines Quotienten ist der Quotient der einzelnen Wurzeln. Natürlich gilt dafür b≠0:

Beispiel:           

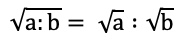
Potenzregel für Wurzeln

• Eine Wurzel kann als Potenz mit Bruch-Exponent geschrieben werden:

Beispiel:        

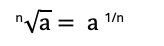
Produktregel für Potenzieren

• Bei gleicher Basis werden die Exponenten addiert.

Beispiel:            a^m*aⁿ = a ^m+n

Quotientenregel für Potenzen

• Bei gleicher Basis werden die Exponenten subtrahiert.

Beispiel:            a^m:aⁿ = a ^m-n

Potenzregel für Potenzen

• Bei Potenzen von Potenzen werden die Exponenten multipliziert.

Beispiel:            (a^m)ⁿ = a ^m*n

Produktregel im Exponenten

• Jede Zahl im Produkt wird einzeln potenziert.

Beispiel:            (a*b)ⁿ = aⁿ*bⁿ

Quotientenregel im Exponenten

• Zähler und Nenner werden einzeln potenziert. Natürlich gilt dafür b≠0:

Beispiel:            (a:b)ⁿ = aⁿ:bⁿ

Aufgaben

3 leichten Aufgaben

1. Vereinfachen Sie die Terme so weit wie möglich:
   1. 12x-y+3z-7x+5y-z=
      1. 8b-3c-7b+3c-b
2. Schreiben Sie die Terme ohne Klammer und vereinfachen Sie so weit wie möglich.
   1. (36u)-(-12v)+(+24v)-(+14u)+(-48v)=
      1. (a+b+c)+(a-b+c)-(a-b-c)=
3. Schreiben Sie ohne Klammer und vereinfachen Sie die Terme so weit wie möglich.
   1. 19b-7a-18x+4-3a-20b+28x-3-10a+7b+5-8a-3x-15=
   1. (7a-2b)-((3a+c)-(2b-3c))=

3 mittelstufige Aufgaben

• Vereinfachen Sie den Term so weit wie möglich.
  • 3a+(2a+3b)*2c+4bc=
  • 7a(2a-3b-4c)2y=
• Löse den folgenden Term
  • (18x²-15xy):(-3x)=
  • (8mn-4m-12m²):(-4m)=
• Löse den folgenden Term
• 2(3a+b)-((b+2c)-(2c+3a))=
• (25u-13v)-(41u-(14u-3(4u-5v)-8v)-7(2u-v))=

3 schwierige Aufgaben

• Berechnen Sie von Hand.

a.  (3/4)²=

b.  (-2)³=

c.   5⁰=

• Löse den folgenden Term
• 4+2³*5-4²:8=
• 100*2:5-2*20+5²*2-10*3=
• 3*(2+5*3+1)+2*(20-5*3-5)-3*0+2=
• Berechnen Sie von Hand.

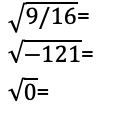
LÖSUNGEN:

1a. Lösung: 5x+4y+2z

Lösungsweg :

12x-y+3z-7x+5y-z=12x-7x-y+5y+3z-z=5x+4y+2z

1b. Lösung:0

Lösungsweg :

8b-3c-7b+3c-b= 8b-7b-b+3c-3c = 0

2a. Lösung: 22u-12v

Lösungsweg :

(36u)-(-12v)+(+24v)-(+14u)+(-48v)= 36u+12v+24v-14u-48v=36u-14u+12v+24v-48v=22u-12v

2b. Lösung: a+b+3c

Lösungsweg:

(a+b+c)+(a-b+c)-(a-b-c)= a+b+c+a-b+c-a+b+c=a+a-a+b-b+b+c+c+c=a+b+3c

3a. Lösung: -28a+6b+7x-9

Lösungsweg:

19b-7a-18x+4-3a-20b+28x-3-10a+7b+5-8a-3x-15=

19b−20b+7b−7a−3a−10a−8a−18x+28x−3x+4−3+5−15=6b-28a+7x-9

3b. Lösung: 4a-4c

Lösungsweg:

(7a-2b)-((3a+c)-(2b-3c))= 7a-2b-(3a+c-2b+3c)=7a-2b-3a-c+2b-3c=

7a-3a-2b+2b-c-3c=4a-4c

4a. Lösung: 3a+4ac+10bc

Lösungsweg:

3a+(2a+3b)*2c+4bc=3a+4ac+6bc+4bc=3a+4ac+10bc

4b. Lösung: 28a^2y-42aby-56acy

Lösungsweg:

7a(2a-3b-4c)2y=(14a²-21ab-28ac)2y=28a²y-42aby-56acy

5a. Lösung: -6x+5y

Lösungsweg:

(18x^2-15xy):(-3x)= -3x(-6x+5y) / -3x = -6x+5y

5b. Lösung: -2n+3m+1

Lösungsweg:

(8mn-4m-12m^2):(-4m)= -4m(-2n+1+3m)/-4m = -2n+1+3m

6a. Lösung: 9a+b

Lösungsweg :

2(3a+b)-((b+2c)-(2c+3a))= 6a+2b-(b+2c-2c-3a)=6a+2b-b-2c+2c+3a=

6a+3a+2b-b-2c +2c=9a+b

6b. Lösung: -13v

Lösungsweg :

(25u-13v)-(41u-(14u-3(4u-5v)-8v)-7(2u-v))= 25u−13v−41u+(14u−3(4u−5v)−8v)+7(2u−v)=

25u−13v−41u+(14u−12u+15v−8v)+7(2u−v)= 25u−13v−41u+(2u+7v)+7(2u−v)= 25u−13v−41u+2u+7v+14u−7v=−13v+7v−7v=−13v

7a. Lösung: 9/16

7.a) Lösung : 9/16

Lösungsweg :

(3/4)²=(3)²/(4)²=9/16

7b. Lösung: -8

Lösungsweg :

(-2)³=(-2)*(-2)*(-2)=-8

7c. Lösung: 1

Lösungsweg:

5⁰=1

8a. Lösung: 3/4

Lösungsweg:

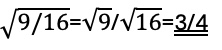
8b. Lösung: nicht definiert

Lösungsweg:

8c. Lösung: 0

Lösungsweg:

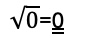
9a. Lösung: 42

Lösungsweg:

4+2³*5-4²:8=4+40-2=42

9b. Lösung: 20

Lösungsweg:

100*2:5-2*20+5²*2-10*3=(100*2:5)-(2*20)+(5²*2)-(10*3)=40-40+50-30=20

9c. Lösung: 56

Lösungsweg:

3*(2+5*3+1)+2*(20-5*3-5)-3*0+2=3⋅18+2⋅0−3⋅0+2=54+0−0+2=56